I just got done with the solve method for the Truss class. As my current PR #23629 which is responsible for initializing the Truss class and I intend on making the changes with respect to the solve method in a different PR, I have, as recommended by my mentor Prakhar, made another folder and cloned the SymPy codebase there as well. So basically, I have two folders to work with: one where I will make changes and test out anything and another one for just pushing the changes that I make in the previous folder by just copy-pasting them. This was, I don’t have to wait for my previous PR to get merged to start work on a new functionality.

Due to this, I was able to start and complete the code for the solve method. I am yet to add tests and documentation for the same and it shouldn’t take much time.

A basic summary of how the solve method is gonna function:

A given truss can be solved if the given condition is met:

\[2n = m + r\]

where \(n\) is the number of nodes, \(m\) is the number of members and \(r\) is the number of reaction loads (if a support is pinned then there are two reaction loads on that support and one reaction load if the support is a roller).

Take the example of the truss that we have been using,

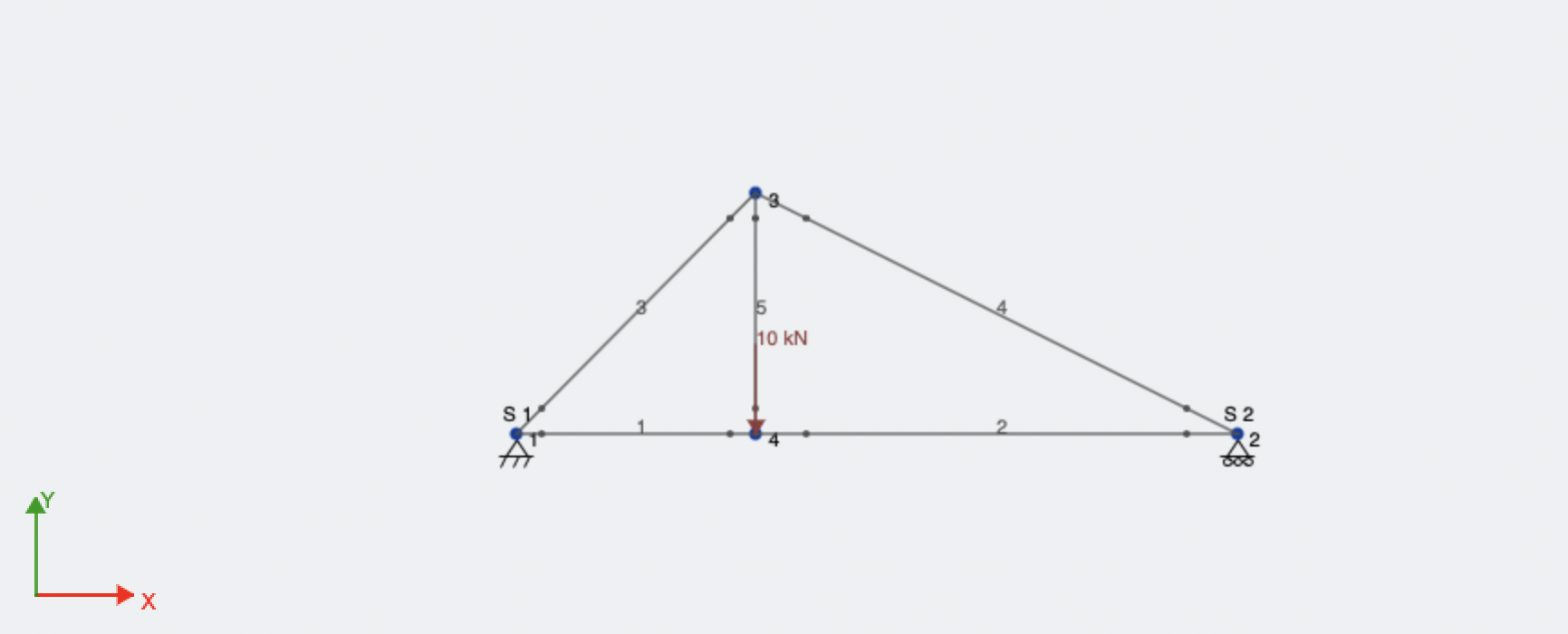
Here, we can basically go over each node and write Equilibrium equations in \(x\) and \(y\). Hence, we get 8 equations. We have 5 members and 1 pinned support and 1 roller support. Hence, 5 internal forces and 3 reaction loads end up giving us 8 variables.

To solve this system of 8 equations and 8 variables, the system must be reduced to a matrix equation of the form,

\[C \cdot F = L\]

Where \(C\) is the Coefficient matrix, \(F\) is the Forces matrix and \(L\) is the Load Matrix.

Hence, the result that we are after is,

\[F = C^{-1} \cdot L\]

The method is all about finding both of these matrices i.e. \(C\) and \(L\) and eventually calculating the result of the Matrix Multiplication.